A Popular Multiple Comparison Test

The analysis of variance has been quite useful in deciding if the results between the means of three or more independent groups are statistically significant or not. It is used in various fields particularly business (e.g, to know if three different types of advertisements affect mean sales differently), agriculture (e.g, to understand whether there is a statistically significant difference in the mean yield that results from these three fertilizers), Medical(e.g, if four different medications lead to different mean blood pressure reductions in patients), Biology(e.g, to know how different levels of sunlight exposure (no sunlight, low sunlight, medium sunlight, high sunlight) and watering frequency (daily, weekly) impact the growth of a certain plant)
While conducting ANOVA, we get a p-value and use it for the interpretation of overall results. If the overall p-value of the ANOVA is lower than our significance level (typically chosen to be 0.10, 0.05, 0.01) then we can conclude that there is a statistically significant difference in mean crop yield between the three fertilizers. We can then conduct post hoc tests (Multiple Comparison Test) to determine exactly which fertilizer leads to the highest mean yield.
Fisher (1935) described a procedure for pairwise comparisons called the least significant difference (LSD) test. It is also called Critical Difference. This test is to be used only if the hypothesis that all means are equal is rejected by the overall F test. If the overall F ratio is not significant, no further tests are performed. When it is used, the two treatments will be declared different if the absolute difference between the two sample means is greater than the LSD at a given level of significance.
The LSD can be calculated by:

where ‘t’ is the student t tabulated value at a given level of significance and degrees of freedom. MSE is the error mean square.
Example:
In order to find out the yielding abilities of five varieties of Sesamum, an experiment was conducted in a greenhouse using a CRD with four plots per variety. The results are:

The ANOVA is:
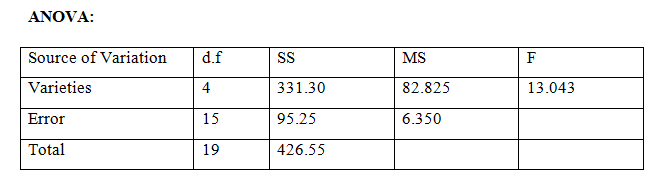
Based on this table, the calculated CD was found to be 3.80.
Checking and evaluating the mean differences of the above yields from different varieties, the results are given as :

I hope you find it useful.
Thank You
